Conheça a matemática recreativa e o paradoxo da área perdida

Muitos problemas matemáticos são estudados apenas porque são divertidos

Jogos e charadas deixam o ensino da disciplina mais interessante e atrativo
Quando estamos com uma pilha de lição de casa de matemática para fazer, ou quando aquele assunto novo tratado pelo seu professor parece impossível de entender, podemos nos esquecer de algo muito importante: como a matemática pode ser divertida. E ela pode, sim, ser fonte de diversão. 
Há todo um ramo da matemática voltado para problemas divertidos. Ele é chamado de matemática recreativa, que frequentemente envolve jogos e charadas. Muitos desses problemas têm alguma aplicação mais séria para outros ramos da matemática. Outros são apenas divertidos.

Um triângulo composto por seis partes

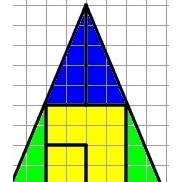
 Vamos conhecer um exemplo de uma charada da matemática recreativa? Ela é chamada de “paradoxo da área perdida”. Observe a imagem ao lado. Temos dois triângulos pequenos, dois triângulos maiores e duas figuras amarelas. Essas figuras se combinam para formar um triângulo grande de base 10 e altura 12.

Rearranjando os componentes do triângulo, fica um espaço em branco no centro

 Imagine que rearranjemos a imagem de modo que os triângulos verdes fiquem em cima, como na imagem ao lado. Note que aconteceu algo muito estranho. Agora há dois quadradinhos no centro que estão em branco. Mas o triângulo resultante também tem base 10 e altura 12. Como isso é possível? De onde veio essa área extra?

Tente encontrar a solução antes de ler o próximo parágrafo.

A resposta é que, na verdade, o triângulo grande formado pelas seis partes não é um triângulo. Os triângulos verde e azul não têm hipotenusas com a mesma inclinação, eles não são triângulos equivalentes. O azul tem base 2 e altura 5, enquanto o verde tem base 3 e altura 7. As medidas dos lados desses triângulos não são proporcionais. Sendo assim, a linha que segue a hipotenusa do triângulo azul e a do verde não é uma linha reta. A consequência é que a área envolvida por essa linha na situação em que o azul está embaixo e o verde em cima é diferente da obtida com o azul em cima e o verde embaixo. A diferença de inclinação é pequena o suficiente para passar despercebida ao olharmos os objetos, mas é grande o suficiente para originar quadrados não preenchidos quando mudamos a configuração dos pedaços envolvidos.
 Gostou? Há muitos outros problemas como esse que são tratados pela matemática recreativa. Pesquise sobre o assunto, pois há muita coisa interessante sendo trabalhada nessa área. O Journal of Recreational Mathematics apresenta novos desenvolvimentos matemáticos nesse tipo de problema. É uma leitura recomendada.