Operações entre conjuntos

DIFERENÇA
Se tomarmos os elementos que pertencem a um determinado conjunto, mas não pertencente a outro, estamos fazendo a diferença entre esses conjuntos. Por exemplo, a diferença entre os conjuntos D e C, simbolizada por D-C, é o conjunto formado pelos elementos de D que não pertencem a C. Ou seja:.
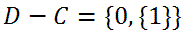
Note que, podemos escrever {1}∈D, pois {1} é elemento de D; e ainda podemos escrever {1}⊂D, pois {1} também é um subconjunto, unitário, de D, já que o elemento 1∈D.

UNIÃO
A união, símbolo “∪”, de dois conjuntos é um outro conjunto cujos elementos pertencem a, pelo menos, um dos dois conjuntos iniciais. Por exemplo,

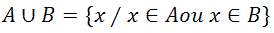
Nesse casso, temos que a união dos conjuntos A={1,2,3,4,5} e B={1,2,6,7,8,9} é o conjunto {1,2,3,4,5,6,7,8,9}, ou seja,
.

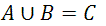
INTERSECÇÃO
Quando um elemento pertence simultaneamente a dois conjuntos, dizemos que este elemento está no conjunto intersecção desses conjuntos. Por exemplo, os elementos da intersecção entre A e B é representada por A∩B e é igual {x⁄x∈Ae x∈B}, que, nesse caso, formam o conjunto {1,2}.
Note que:

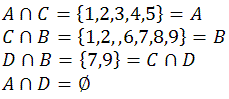
* ∅ é o símbolo para o conjunto vazio. Este conjunto não possui elementos e, por isso, ∅ está contido em qualquer outro conjunto, por exemplo, ∅⊂A.

Fechar janela

Clique aqui para baixar o arquivo original

Diferença de conjuntos

DIFERENÇA
Se tomarmos os elementos que pertencem a um determinado conjunto, mas não pertencente a outro, estamos fazendo a diferença entre esses conjuntos. Por exemplo, a diferença entre os conjuntos D e C, simbolizada por D-C, é o conjunto formado pelos elementos de D que não pertencem a C. Ou seja:
.
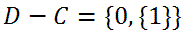
Note que, podemos escrever {1}∈D, pois {1} é elemento de D; e ainda podemos escrever {1}⊂D, pois {1} também é um subconjunto, unitário, de D, já que o elemento 1∈D.

 

Fechar janela

Clique aqui para baixar o arquivo original

União entre conjuntos

UNIÃO
A união, símbolo “∪”, de dois conjuntos é um outro conjunto cujos elementos pertencem a, pelo menos, um dos dois conjuntos iniciais. Por exemplo,

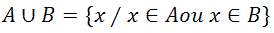
Nesse casso, temos que a união dos conjuntos A={1,2,3,4,5} e B={1,2,6,7,8,9} é o conjunto {1,2,3,4,5,6,7,8,9}, ou seja,
.

Fechar janela

Clique aqui para baixar o arquivo original

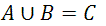
Intersecção de conjuntos

INTERSECÇÃO
Quando um elemento pertence simultaneamente a dois conjuntos, dizemos que este elemento está no conjunto intersecção desses conjuntos. Por exemplo, os elementos da intersecção entre A e B é representada por A∩B e é igual {x⁄x∈Ae x∈B}, que, nesse caso, formam o conjunto {1,2}.
Note que:

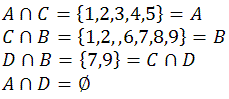
* ∅ é o símbolo para o conjunto vazio. Este conjunto não possui elementos e, por isso, ∅ está contido em qualquer outro conjunto, por exemplo, ∅⊂A.